Simulation in Games: Week 1
Starting today, I’m going to be keeping a weekly blog of my learning and progress in the Simulation in Games module! This will include a closer look at the week’s topic (and my understanding of it), exercises relating to said topic and the state of the game I am producing as part of the assignment. All of these will be discussed in the context of the Unity game engine and C#. Let’s get into it then, shall we?
Maths, Vectors and Distance
Maths
This week’s practical started off with examining some basic Maths functions. In Unity, most of these are already implemented as part of the Mathf struct.
-
Random numbers - These are implemented as part of the Random class, specifically its static method Range(). This can return either an integer or a float number between the two numbers passed in as parameters. Very useful when trying to create a random spawning pattern, for example.
-
Range conversion - To convert a number from one range to another, one can use the following formula:
newValue = (oldValue - minOld) / ((minNew - minOld) * (maxNew - maxOld) + maxOld); -
The square root of a number - Can be found using the Mathf method Sqrt(). Sqrt() returns a float.
-
Exponentiation - A Mathf method, Pow(). The first parameter is the base, the second parameter is the exponent. Pow() returns a float.
-
Angles - Mathf contains methods for trigonometric functions, such as Sin() and Cos(). These methods work in radians. To convert an angle in degrees to one in radians, one can multiply the angle by the Mathf constant Deg2Rad or (Mathf.PI / 180). Conversion from an angle in radians to one in degrees is also possible by multiplying the angle by Rad2Deg or (180 / Mathf.PI). Angles can be used for projectile motion and trigonometric functions are useful for simple harmonic motion.
Vectors
Vectors are geometric objects that have a magnitude and a direction. In Unity, Vectors are represented by several structs: Vector2, Vector3, Vector4 and their Int equivalents (except Vector4, which doesn’t have an Int equivalent).
-
Addition / Subtraction - Vectors can very simply be added together using the ‘+’ operator and subtracted using the ‘-‘ operator. If adding or subtracting vectors of differing dimensions together (a Vector3 and a Vector2, for example), casting will have to be used on one of the vectors.
-
Multiplication / Division - A vector can be multiplied (‘*’ operator) or divided by (‘/’ operator) a float. A vector can also be scaled by another vector using the Scale() method.
-
Directional vectors - A directional vector is the vector between a point A and a point B. To calculate it, one must simply subtract one from the other. To get the direction from B to A, subtract
A - Band vice versa.
Distance
Distance is the numerical measurement of how far apart objects are. In game development, distance can be used to implement enemy line of sight / aggro, among other things. The formula for calculating distance is (Vector2):

In Unity, this formula can be represented as a method (Vector3):
{
return Mathf.Sqrt(Mathf.Pow(b.x - a.x, 2) + Mathf.Pow(b.y - a.y, 2) + Mathf.Pow(b.z - a.z, 2));
}
Of course, Unity already has methods for calculating Distance as part of the Vector structs. However, for the sake of the module, we were asked to look at the underlying formulas and to reimplement them ourselves. I have thus implemented the above method as part of my own struct, PhysicsCalc.
Exercise - An Application of Distance
The Tasks
For this week’s practical, we were tasked with creating a Unity project that:
- Contains a cube, Cube A, at coordinates (5, 3, 7).
- Produces N number of primitives with a random position within a range of (-10, 10) for each coordinate, where N is a number defined by the user at runtime.
- Deletes, or skips the creation of those primitives that are M units or less away from Cube A’s position, where M is a number defined by the user at runtime.
- Displays how many primitives remain in the console after action 3 (excluding Cube A).
- Creates a cube, Cube B, at random coordinates when W is pressed and calculates, displays in the console and draws the directional vector from Cube A to Cube B.
Actions 2, 3 and 4 above should happen after Spacebar is pressed.
The Implementation
Primitives
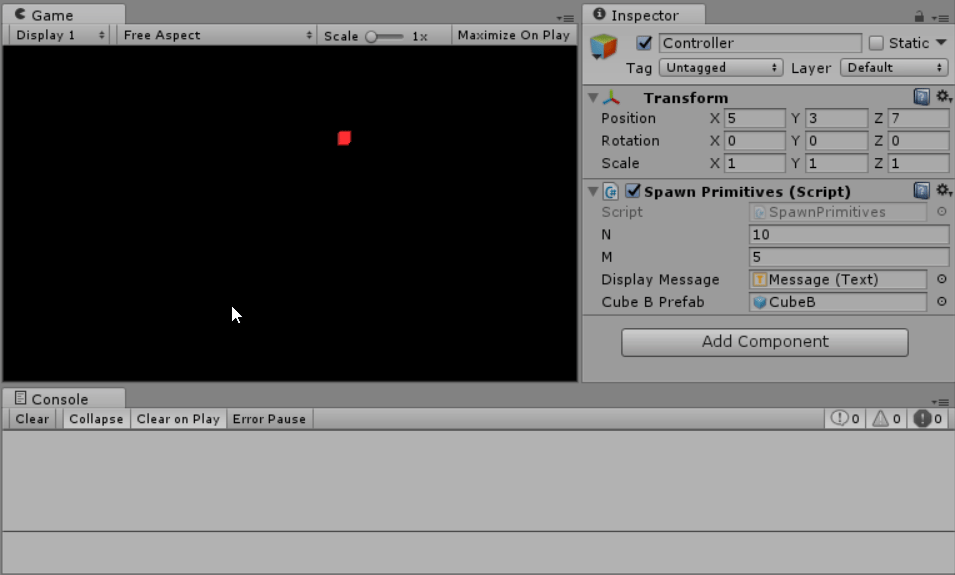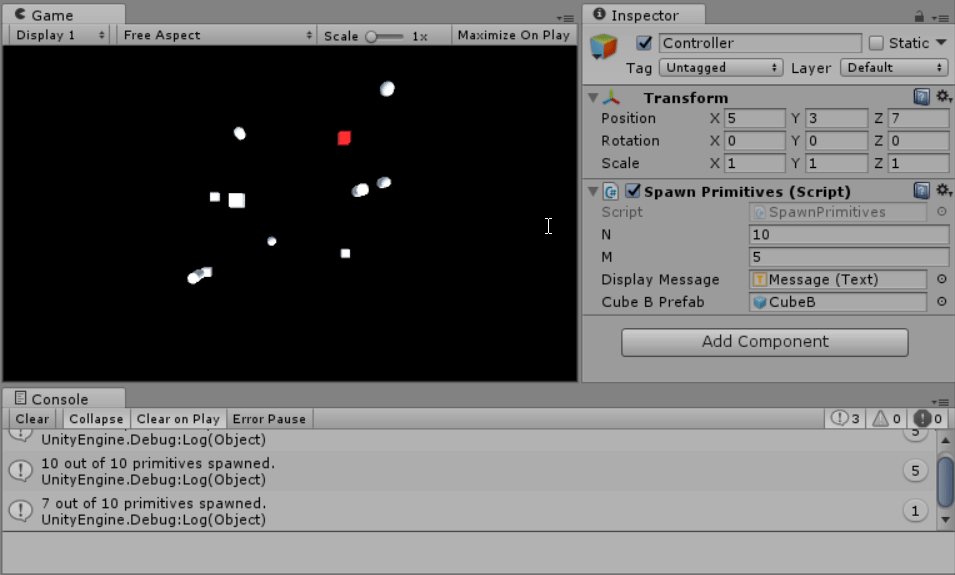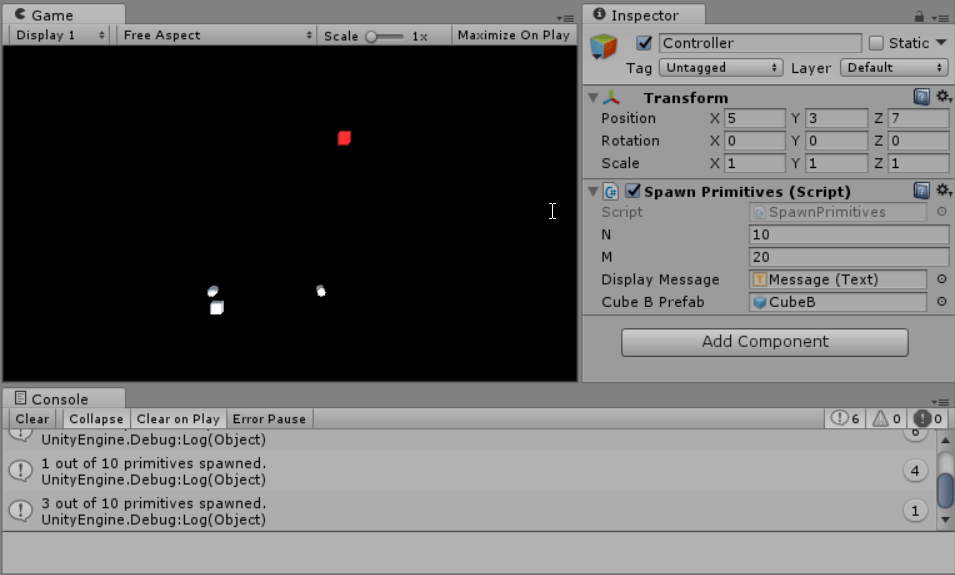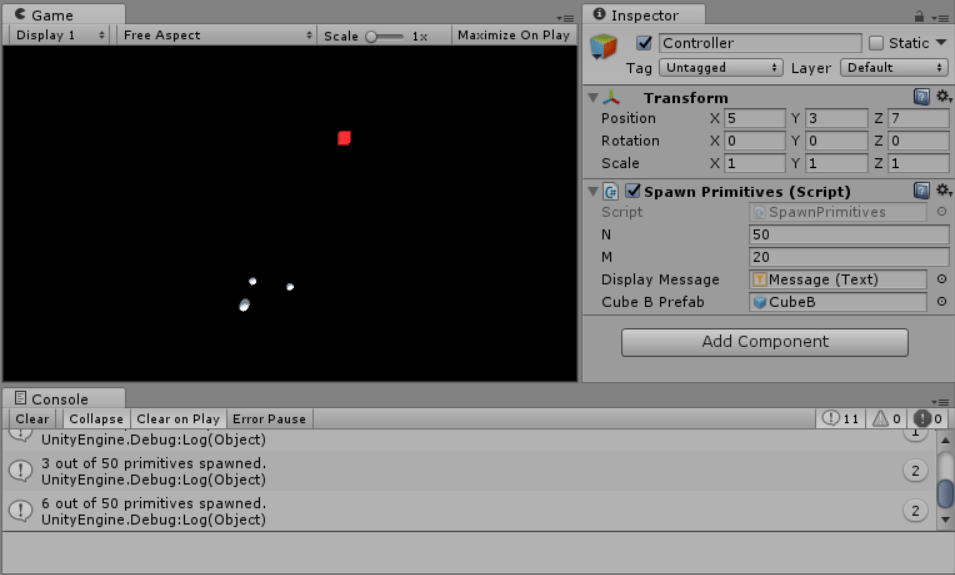
For actions 1-4, I wrote a method which, after Spacebar is pressed, picks a location within the (-10, 10) range at random. Afterwards, the method checks if the location is too close to Cube A using the previously mentioned distance method.
-
If it is, no primitive is spawned.
-
If it isn’t, a primitive is spawned at the location and added to a list of primitives. All primitives in this list are destroyed the next time Spacebar is pressed, and the list itself is cleared.
Cube B

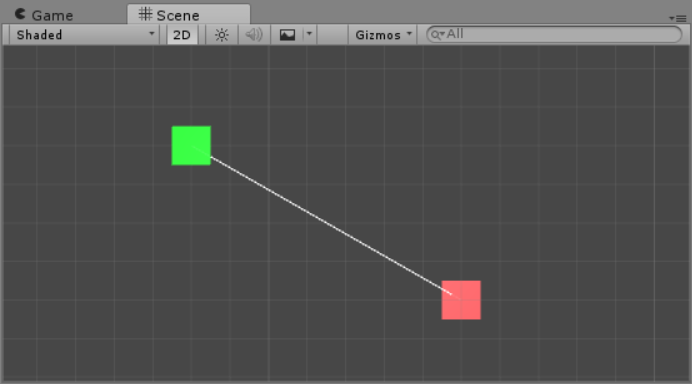
For action 5, the method first checks if Cube B was spawned previously. If the answer is yes, it is destroyed. Then, Cube B is instantiated and placed at a random location. Soon after, the directional vector between Cube B and Cube A is calculated and drawn by subtracting Cube A’s position from Cube B’s.
Witchcraft Academy (working title)
The assignment for the module requires that we produce a game that demonstrates the application of the physics concepts we learn. My current idea is a game where the player takes control of a wizard who uses physics spells to manipulate the environment around him to defeat enemies and / or solve puzzles as part of a wizard graduation ceremony. Tune in next week to learn more. Thanks for reading!